Maximizing Social Strategic Diffusion

As online social networking service became popular, people are more actively using social network to share opinions on new products or information. Due to this, companies could have new marketing opportunities to use social network via accessing social network datasets. We have worked on understanding algorithmic perspectives of social networks to advance such opportunities. In this line of works, to understand the social diffusion, we model the strategic behavior as a networked coordination game and study the prominent feature in the social diffusion. In particular, according to our analysis on the game diffusion model, it turns out that clustering structure of social networks, which is often observed in reality (see the following figure), plays an important role.

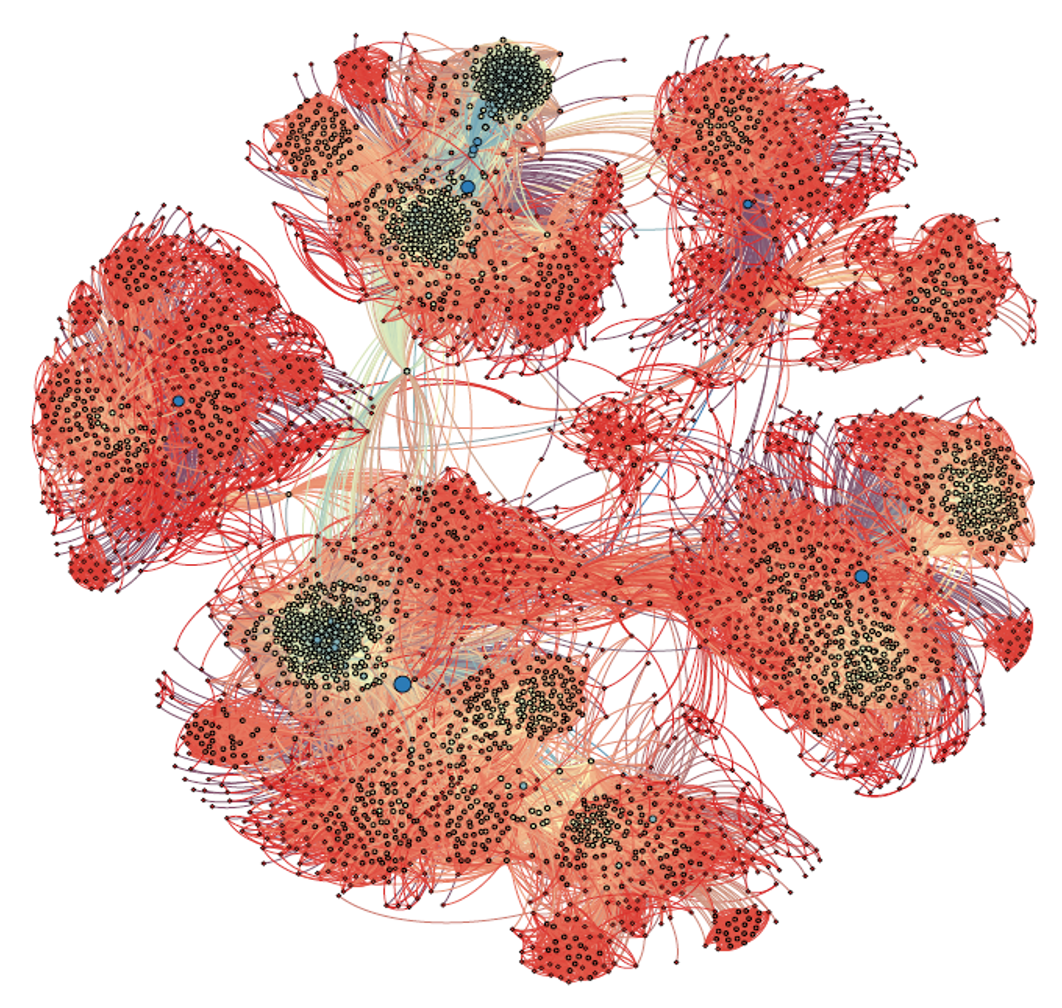: A social graph in Facebook consisting of 4,039 users and 88,234 edges and having average clustering coefficient 0.6055 and degree distribution fit into power law distribution with exponent 1.18.

We first study how to design social marketing strategy to spread new products where the marketing strategy depends on the clustering structure in social networks by studying the seeding problem in various game-based diffusion models. In particular, we addressed the seeding problem in the most classical game-based progressive and non-progressive diffusion models by the diffusion time minimization problem. According to our analysis, the clustering structure in social graph is the most important feature in the diffusion pattern thus for given seeding budget, the optiaml seed users can be selected by simple mechanism being aware of the clustering structure.

On Maximizing Diffusion Speed over Social Networks with Strategic Users

Jungseul Ok, Youngmi Jin, Jinwoo Shin and Yung Yi
IEEE/ACM Transactions on Networking, vol. 24, no. 6, pp. 3798-3811, 2016 (preliminary version appeared in SIGMETRICS 2014)

On the Progressive Spread over Strategic Diffusion: Asymptotic and Computation

Jungseul Ok, Jinwoo Shin and Yung Yi
INFOCOM 2015

We also studied a more practical scenario of the seeding problem where, for given marketing budget, we can control number of seeds and incentive per each seed while the amount of incentive per seed is fixed. % before this work, i.e., the number of seeds is given instead of the marketing budget. To do so, we proposed a new incentive model and characterize the speed of diffusion as a certain combinatorial optimization task. Then, we apply the characterization to popular network graph topologies (Erdős-Rényi, planted partition and power law graphs) as well as general ones. Our analysis shows that the diffusion time undergoes two levels of order-wise reduction, where the first and second one are solely contributed by the number of seeded users, i.e., quantity, and the amount of incentives, i.e., quality, respectively. In other words, it implies that the best strategy given budget is (a) first identify the minimum seed set depending on the underlying graph topology, and (b) then assign largest possible incentives to users in the set.

Incentivizing Strategic Users for Social Diffusion: Quantity or Quality?

Jungseul Ok, Jinwoo Shin and Yung Yi
INFOCOM 2017

Despite of our efforts to maximizing the speed of social strategic diffusion, it is often exponentially slow with respect to the network size. We also introduced an interesting concept called ‘herd mentality’, which can alleviate the issue.

Dynamics in Congestion Games

Devavrat Shah and Jinwoo Shin
SIGMETRICS 2010

(edited by Jungseul Ok and Jinwoo Shin, Dec 2016)